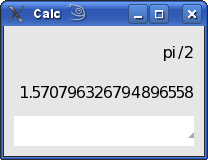
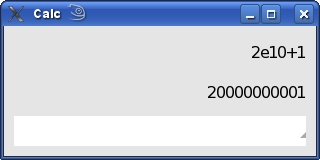
| abs | абсолютное значение |x| |
| floor | целая часть числа [x] (полeng) |
| floor(x,n) | целая часть деления [x/n] |
| ceil | минимальное целое число не меньшее x (потолокeng) |
| gcd(x,…,z) | наибольший общий делитель целых чисел |
| lcm(x,…,z) | наименьшее общее кратное целых чисел |
| sqrt(x[,eps]) | квадратный корень √x [с указанной относительной точностью result*(1-eps)..result*(1+eps)]. По умолчанию точность 2-64. |
| cbrt(x[,eps]) | кубический корень ∛x [с указанной относительной точностью result*(1-eps)..result*(1+eps)]. По умолчанию точность 2-64. |
| exp | экспонента ex |
| ln(x[,eps]) | логарифм натуральный [с указанной точностью result-eps..result+eps]. По умолчанию точность 2-64. |
| log(base,x) | логарифм с основанием base: logbase(x) |
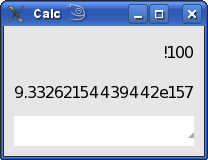
| ! | факториал x! |
| sin(x[,eps]) | синус [с указанной точностью result-eps..result+eps]. По умолчанию точность 2-64. |
| cos(x[,eps]) | косинус [с указанной точностью result-eps..result+eps]. По умолчанию точность 2-64. |
| tan | тангенс tan(x) |
| cot | котангенс cot(x) |
| arcsin | арксинус sin-1(x) |
| arccos | арккосинус cos-1(x) |
| arctan | арктангенс tan-1(x) |
| arctan(y,x) | арктангенс от деления tan-1(y/x) |
| sinh | синус гиперболический sinh(x) |
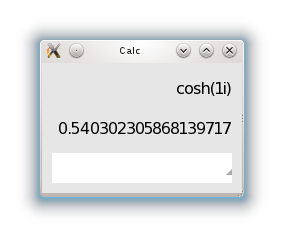
| cosh | косинус гиперболический cosh(x) |
| tanh | тангенс гиперболический tanh(x) |
| coth | котангенс гиперболический coth(x) |
| arsinh | арксинус гиперболический sinh-1(x) |
| arcosh | арккосинус гиперболический cosh-1(x) |
| artanh | арктангенс гиперболический tanh-1(x) |
| degrees | =x*180/π |
| radians | =x/180*π |
| combin(x,n) | =C(x,n)=n!/x!/(n-x)! |
| combina(x,n) | =n!/(n-x)! |
| multinomial(x,…,z) | =(x+…+z)!/x!…/z! |
| erf(x) | функция ошибок Гаусса: 2/√π∫0x(e-t2)ⅆt |
| num(x) | числитель |
| denom(x) | делитель |
| round(x) | округление до целого числа |
| round(x,y) | округление в пределах [x-y,x+y] |
| real(x) | действительная часть комплексного числа |
| imag(x) | мнимая часть комплексного числа |
| random(макс) | случайное вещественное число, меньшее по абсолютному значению, чем макс |
| randomcomplex(x) | комплексное число, меньшее по абсолютному значению, чем abs|x| |
| randomnormal(среднее,отклонение) | случайное число, с нормальным распределением |